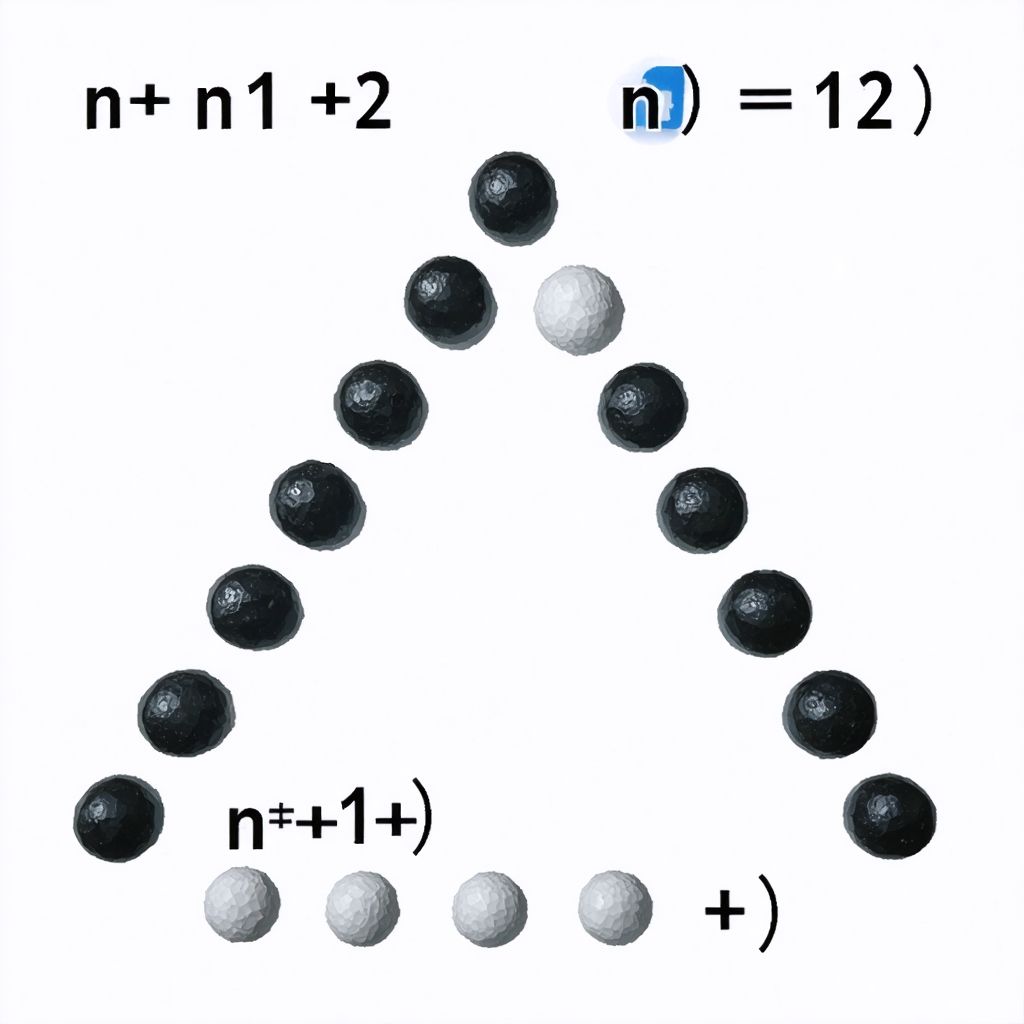Tiempo estimado de lectura: 15 minutos | Matemáticas |
Explorando los misterios de los números triangulares: definición, cálculo y aplicaciones
Descubriendo la magia matemática de los números triangulares
Los números triangulares representan uno de los conceptos más elegantes y visuales de las matemáticas, donde la aritmética y la geometría se encuentran de manera perfecta. Estos números especiales han fascinado a matemáticos durante más de 2.500 años, desde los antiguos pitagóricos hasta los investigadores contemporáneos en teoría de números y ciencias de la computación.
¿Te has preguntado alguna vez por qué ciertos números aparecen repetidamente en la naturaleza y en patrones matemáticos? Los números triangulares ofrecen una ventana única hacia la comprensión de estos patrones universales, revelando conexiones profundas entre conceptos aparentemente dispares.
¿Qué son los números triangulares? Definición completa y conceptos fundamentales
Definición matemática precisa
Un número triangular es un número natural que puede expresarse como la suma de los primeros n números naturales consecutivos, donde n ≥ 1. Matemáticamente, el n-ésimo número triangular se define como:
Tn = 1 + 2 + 3 + … + n = Σ(k=1 to n) k
Representación geométrica y visual
La belleza de los números triangulares radica en su representación visual. Imagina puntos dispuestos en filas que forman un triángulo equilátero perfecto:
- T₁ = 1: Un solo punto (●)
- T₂ = 3: Tres puntos formando un triángulo pequeño
- T₃ = 6: Seis puntos en configuración triangular
- T₄ = 10: Diez puntos manteniendo la forma triangular
Esta representación visual no es meramente decorativa; revela propiedades matemáticas profundas que conectan la geometría con la aritmética de manera fundamental.
Secuencia de los números triangulares
La secuencia completa de los primeros números triangulares es:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210…
Cada término en esta secuencia tiene propiedades únicas y conexiones sorprendentes con otros conceptos matemáticos.
Cómo calcular un número triangular: un proceso sencillo
Calcular un número triangular es más fácil de lo que podrías imaginar. La fórmula Tn = n(n + 1) / 2 es la clave para desvelar el valor de cualquier número triangular, sin necesidad de dibujar triángulos ni contar puntos. Este cálculo, aunque simple en su estructura, esconde una profunda conexión con la suma de números naturales, un concepto fundamental en matemáticas.
Pasos detallados para el cálculo
- Identifica el valor de «n»: Determina la posición del número triangular que deseas calcular (por ejemplo, si quieres calcular el 5º número triangular, n = 5).
- Aplica la fórmula: Sustituye el valor de «n» en la fórmula Tn = n(n + 1) / 2.
- Resuelve la ecuación: Realiza las operaciones matemáticas para obtener el resultado. Primero, multiplica «n» por (n + 1), y luego divide el resultado entre 2.
- El resultado es el número triangular: El número obtenido es el valor del número triangular en la posición «n».
Ejemplo práctico: calculando el décimo número triangular
Para ilustrar el proceso, calculemos el décimo número triangular (T₁₀). Siguiendo los pasos anteriores:
Paso 1: n = 10 (queremos calcular el décimo número triangular)
Paso 2: T₁₀ = 10(10 + 1) / 2
Paso 3: T₁₀ = 10 * 11 / 2 = 110 / 2 = 55
Resultado: El décimo número triangular es 55. Esto significa que puedes formar un triángulo con 55 puntos.
Métodos alternativos para explorar los números triangulares (para los más curiosos)
Si bien la fórmula principal es la más práctica, existen otras formas de entender y calcular los números triangulares:
Método Recursivo: Cada número triangular se puede obtener sumando su posición (‘n’) al número triangular anterior (Tn-1).
Fórmula: Tn = T(n-1) + n
Condición inicial: T₁ = 1
Ejemplo: Para calcular T₄: T₄ = T₃ + 4. Si sabemos que T₃ = 6, entonces T₄ = 6 + 4 = 10.
Método Combinatorio: Un número triangular Tn también es igual al número de maneras de elegir 2 elementos de un conjunto de (n+1) elementos. Esto se conoce como combinaciones «n+1 tomados de a 2».
Fórmula: Tn = C(n+1, 2) = (n+1)! / (2! * (n+1-2)!) = (n+1)! / (2! * (n-1)!)
Simplificando: (n+1) * n * (n-1)! / (2 * 1 * (n-1)!) = (n+1)n / 2
Esto nos lleva de nuevo a la fórmula principal.
Por Diferencias Finitas: Si observas la secuencia de números triangulares (1, 3, 6, 10, 15, 21…), las diferencias entre términos consecutivos (3-1=2, 6-3=3, 10-6=4…) forman la secuencia de los números naturales (2, 3, 4, 5…). Esta propiedad es característica de las secuencias polinómicas de segundo grado.
La derivación de la fórmula: un vistazo a su fundamento matemático
La fórmula para calcular los números triangulares no es una invención arbitraria; tiene una base matemática sólida que se deriva de la suma de los primeros números naturales. Esta relación se manifiesta a través de un ingenioso truco matemático que, como la leyenda de Gauss, simplifica el proceso de suma.
La clave para entender la fórmula n(n + 1) / 2 reside en la idea de emparejar los números. Si queremos sumar los números del 1 al n, podemos emparejar el primer número (1) con el último (n), el segundo (2) con el penúltimo (n-1), y así sucesivamente. Cada par sumará (n + 1). Si «n» es par, tendremos exactamente n/2 pares, y la suma total será (n/2) * (n + 1). Si «n» es impar, tendremos (n-1)/2 pares, y el número del centro que no se empareja, que es (n + 1)/2. Si sumamos estos números, obtenemos (n-1)/2 * (n+1) + (n+1)/2, que es igual a n(n + 1) / 2. De este modo, demostramos que la fórmula que utilizamos para calcular los números triangulares es correcta, no es una mera coincidencia.
Propiedades matemáticas avanzadas de los números triangulares
Aunque su definición es sencilla y su forma visual evocadora, los números triangulares esconden un conjunto de propiedades profundas que han fascinado a matemáticos durante siglos. Estas propiedades van mucho más allá de su representación geométrica y nos llevan a conexiones con otras figuras numéricas, patrones de divisibilidad y relaciones sorprendentes dentro del universo de las matemáticas.
Propiedades algebraicas fundamentales
1. Suma de dos números triangulares consecutivos
Una de las propiedades más llamativas es que si sumas un número triangular con el siguiente en la secuencia, el resultado es siempre un número cuadrado perfecto. Por ejemplo, 3 (el segundo número triangular) más 6 (el tercero) da 9, que es un cuadrado (3 × 3). Esto significa que la unión de dos triángulos consecutivos puede formar un cuadrado completo, tanto visual como matemáticamente.
2. Diferencia entre números triangulares
La diferencia entre dos números triangulares consecutivos siempre es igual al número de orden del más reciente. Por ejemplo, 10 (el cuarto número triangular) menos 6 (el tercero) da 4. Esto se debe a que en cada paso de la secuencia se añade una fila más de puntos.
3. Producto de números triangulares
A diferencia de la suma o la diferencia, el producto de dos números triangulares no produce necesariamente otro número triangular. Por ejemplo, multiplicar 3 por 6 da 18, que no pertenece a la secuencia de los triangulares. Este comportamiento demuestra que los números triangulares no están cerrados bajo la operación de multiplicación.
4. Paridad y patrones modulares
Los números triangulares también presentan patrones interesantes en cuanto a su paridad (si son pares o impares). Un número triangular será par si su posición en la secuencia es múltiplo de 4, o si esa posición deja un resto de 1 al dividirse por 4. En los demás casos, será impar. Este tipo de comportamiento es útil para crear algoritmos y modelos matemáticos eficientes.
Relaciones con otros números figurados
Los números triangulares forman parte de una familia más amplia de números llamados «figurados», que incluyen a los cuadrados, pentagonales, hexagonales y tetraédricos. Cada uno representa una forma geométrica construida con puntos.
1. Relación con los números cuadrados
Existe una conexión muy curiosa: si tomamos un número triangular, lo multiplicamos por ocho y le sumamos uno, el resultado siempre será un cuadrado perfecto. Por ejemplo, si usamos el número triangular 6, obtenemos 49, que es 7 al cuadrado. Este tipo de relaciones permite unir diferentes estructuras numéricas en un mismo marco teórico.
2. Conexión con los números pentagonales
Los números pentagonales, que representan puntos formando un pentágono, tienen vínculos con los triangulares a través de ciertas fórmulas. Aunque no todos los números triangulares son también pentagonales, existen algunos que pertenecen a ambas secuencias. Encontrarlos implica resolver ecuaciones más complejas, lo cual ha sido un reto clásico en la historia de la teoría de números.
3. Relación con los números tetraédricos
Los números tetraédricos pueden verse como una extensión tridimensional de los números triangulares. Mientras que los triangulares forman triángulos planos, los tetraédricos forman pirámides de puntos con base triangular. Estos se obtienen sumando los primeros números triangulares, es decir, apilando triángulos uno encima del otro. Así, se pasa de una figura en dos dimensiones a una en tres.
Propiedades en teoría de números
Además de sus vínculos geométricos, los números triangulares presentan comportamientos interesantes en el campo de la teoría de números, especialmente en lo que respecta a la divisibilidad y las propiedades modulares.
1. Divisibilidad por 3
No todos los números triangulares son divisibles por 3, pero hay un patrón: un número triangular será divisible por 3 si su posición en la secuencia también cumple una determinada condición. Por ejemplo, los números triangulares en las posiciones 3, 5, 6, 8 y 9 sí lo son, lo que indica una estructura interna repetitiva.
2. Números triangulares que también son cuadrados perfectos
Hay algunos números excepcionales que son a la vez triangulares y cuadrados. Es decir, pueden representarse tanto como triángulos formados por puntos como cuadrados perfectos. Algunos ejemplos son el 1, el 36 o el 1225. Estos casos son escasos, pero han sido objeto de estudio por su singularidad. Descubrirlos implica resolver problemas matemáticos que forman parte de la llamada teoría de ecuaciones diofánticas.
3. Conjetura de Polignac y conexiones con los números primos
Una de las conjeturas más interesantes, aunque no resuelta, plantea que ciertos números triangulares podrían estar relacionados con los números primos. Por ejemplo, existen pares de primos cuya suma o diferencia da como resultado un número triangular. Estas relaciones, aunque aún en estudio, apuntan a una conexión profunda entre las estructuras aritméticas aparentemente dispares.
Una puerta a las matemáticas profundas
Los números triangulares son mucho más que una simple suma de números naturales. Representan una entrada accesible pero poderosa al mundo de la matemática avanzada. A través de sus propiedades, nos permiten explorar conceptos clave en álgebra, geometría, teoría de números y lógica. Al observar sus patrones, conexiones y transformaciones, abrimos una ventana hacia las estructuras invisibles que dan forma a las matemáticas, tanto en su dimensión estética como en su potencial aplicado.
Un viaje a través del tiempo: la historia y evolución de los números triangulares
Los números triangulares, con su elegante simplicidad y profunda conexión con la estructura fundamental de las matemáticas, no son un descubrimiento reciente. Su estudio se remonta a los albores de la civilización, evolucionando a través de los siglos gracias a la curiosidad y el ingenio de grandes mentes.
1. Los orígenes místicos: los pitagóricos (siglo VI a.C.)
El viaje de los números triangulares comienza en la Antigua Grecia, en el seno de la escuela pitagórica. Liderados por el enigmático Pitágoras, estos filósofos y matemáticos veían el universo como una manifestación de los números. Para ellos, los números no eran meras abstracciones, sino la esencia misma de la realidad, con propiedades místicas y divinas.
Números Figurados: Los pitagóricos fueron pioneros en el estudio de los números figurados, clasificando los números según las formas geométricas que podían representar al disponer guijarros o puntos. Los números triangulares fueron uno de los primeros y más importantes tipos, junto con los cuadrados, pentagonales, etc.
Cosmos y Armonía: Veían en estos patrones numéricos una representación de la armonía del cosmos y una conexión tangible entre las matemáticas abstractas y el mundo natural. Estudiar los números triangulares era, en parte, una forma de comprender el orden subyacente del universo.
El Tetraktys: Un símbolo sagrado para los pitagóricos era el Tetraktys, una figura triangular compuesta por diez puntos (1+2+3+4 = 10, el cuarto número triangular). Representaba conceptos metafísicos fundamentales y era objeto de veneración.
2. Contribuciones luminarias: gigantes de la matemática
Tras sus inicios en la Grecia clásica, el estudio de los números triangulares y sus propiedades continuó fascinando a matemáticos a lo largo de la historia.
Arquímedes de Siracusa (c. 287 – c. 212 a.C.): Aunque no se centró exclusivamente en ellos, Arquímedes utilizó conceptos relacionados con sumas de series (fundamentales para los números triangulares) en sus trabajos sobre áreas y volúmenes, demostrando un profundo entendimiento de estos principios.
Nicómaco de Gerasa (c. 60 – c. 120 d.C.): En su obra «Introducción a la Aritmética», Nicómaco detalló las propiedades de los números figurados, incluyendo los triangulares, ayudando a preservar y transmitir el conocimiento pitagórico a generaciones posteriores.
Pierre de Fermat (1607-1665): Este brillante matemático francés hizo una contribución notable con su Teorema de los Números Triangulares de Fermat (también conocido como el Teorema de los Números Poligonales de Fermat para el caso triangular). Afirmó, y más tarde fue demostrado por Gauss, que todo número entero positivo puede expresarse como la suma de, como máximo, tres números triangulares. Por ejemplo, 17 = 10 (T₄) + 6 (T₃) + 1 (T₁). Esto reveló una estructura profunda y sorprendente dentro del sistema numérico.
Carl Friedrich Gauss (1777-1855): A menudo llamado el «Príncipe de los Matemáticos», Gauss protagonizó una famosa anécdota de su niñez. Con tan solo 9 o 10 años, su maestro pidió a la clase sumar todos los números del 1 al 100. Gauss encontró la respuesta (5050) en segundos, al darse cuenta de que podía emparejar los números (1+100=101, 2+99=101, …, 50+51=101), habiendo 50 de tales pares. Esto es, esencialmente, una derivación intuitiva de la fórmula n(n+1)/2 para T₁₀₀. Este episodio no solo muestra su genio precoz, sino también la potencia inherente al concepto de número triangular.
Leonhard Euler (1707-1783): Uno de los matemáticos más prolíficos de la historia, Euler exploró exhaustivamente las propiedades de los números y las series. Investigó las funciones generatrices, herramientas poderosas que pueden encapsular secuencias enteras (como los números triangulares) en una sola expresión. Su trabajo conectó los números triangulares con áreas más avanzadas del análisis matemático y la teoría de números, estableciendo bases para el estudio moderno de las secuencias.
3. La era digital y desarrollos modernos (siglos XX-XXI)
Lejos de ser una mera curiosidad histórica, los números triangulares y los principios subyacentes a su cálculo siguen siendo relevantes y han encontrado nuevas aplicaciones en la era moderna y digital:
Teoría de Grafos: En la teoría de grafos, un grafo completo K<sub>n</sub> (un grafo donde cada par de vértices distintos está conectado por una arista única) tiene T<sub>(n-1)</sub> = (n-1)n/2 aristas. Esto es crucial para analizar redes, desde sociales hasta de comunicaciones. Por ejemplo, para saber cuántas conexiones directas hay en un grupo de ‘n’ personas donde todas se conocen, usarías esta idea.
Ciencias de la Computación y Análisis de Algoritmos: La suma de los primeros ‘n’ enteros (es decir, el n-ésimo número triangular) aparece frecuentemente al analizar la complejidad de algoritmos, especialmente aquellos que involucran bucles anidados. Comprender esto ayuda a estimar el tiempo de ejecución y la eficiencia de los programas.
Combinatoria y Probabilidad: Los números triangulares son un caso especial de coeficientes binomiales (T<sub>n</sub> = C(n+1, 2)), que son fundamentales en combinatoria (el arte de contar) y, por extensión, en probabilidad. Se utilizan para calcular el número de pares que se pueden seleccionar de un conjunto, como en el famoso problema del «apretón de manos».
Criptografía y Seguridad: Aunque no directamente, las propiedades de la teoría de números, donde los números figurados como los triangulares tienen su lugar, son la base de muchos algoritmos criptográficos modernos. La dificultad de factorizar números grandes o resolver ciertos problemas de teoría de números sustenta la seguridad de las comunicaciones digitales.
Modelado y Simulación: En diversas disciplinas científicas y de ingeniería, los patrones que involucran sumas acumulativas o estructuras triangulares pueden aparecer en modelos de crecimiento, distribución o interacciones.
Inteligencia Artificial y Aprendizaje Automático: Si bien las aplicaciones directas pueden ser específicas, los principios de combinatoria, optimización y análisis de estructuras de red (donde los números triangulares pueden surgir) son fundamentales en el diseño y la optimización de arquitecturas de redes neuronales y algoritmos de aprendizaje.
En conclusión, la historia de los números triangulares es un testimonio de la continuidad del pensamiento matemático. Lo que comenzó como una observación geométrica y filosófica en la Antigua Grecia ha evolucionado, enriqueciéndose con los aportes de grandes matemáticos y encontrando aplicaciones prácticas e insospechadas en el corazón de nuestra tecnología digital moderna. Son un recordatorio de que incluso los conceptos matemáticos más simples pueden albergar una profunda belleza y una utilidad duradera.
Datos curiosos: descubriendo curiosidades sobre los números triangulares
Los números triangulares no solo poseen un encanto visual y una importancia teórica dentro de las matemáticas; también están rodeados de anécdotas históricas, apariciones en la naturaleza y conexiones sorprendentes con otras áreas del conocimiento. A continuación, exploramos algunas curiosidades que revelan lo asombrosamente versátiles que pueden ser.
El Joven Gauss y la Suma Rápida
Una de las historias más célebres de la historia de las matemáticas tiene como protagonista a Carl Friedrich Gauss, considerado uno de los genios más grandes de esta ciencia. Siendo apenas un niño en la escuela primaria, su profesor le pidió a la clase que sumara los números del 1 al 100, quizás con la intención de mantenerlos ocupados un buen rato. Para sorpresa de todos, Gauss dio la respuesta correcta (5050) en cuestión de segundos.
¿Cómo lo hizo? Se dio cuenta de un patrón triangular: al emparejar el primer número con el último (1 + 100), el segundo con el penúltimo (2 + 99), y así sucesivamente, obtenía siempre la misma suma. Solo tenía que multiplicar el número de pares por el resultado de cada suma. Este razonamiento está directamente ligado a la naturaleza de los números triangulares, ya que sumar los números del 1 al n es precisamente lo que define un número triangular.
Números Triangulares en la Naturaleza
Aunque los números triangulares son una creación humana en términos de simbolismo, la naturaleza parece «reconocer» sus patrones. En la disposición de algunos elementos biológicos, podemos encontrar configuraciones que coinciden con secuencias triangulares:
Semillas en flores: En girasoles o margaritas, la forma en que las semillas están distribuidas suele seguir patrones espirales que, al analizarse, revelan estructuras que coinciden con números figurados, entre ellos los triangulares.
Panales de abejas: Aunque la forma dominante en los panales es el hexágono, su construcción implica agrupaciones de puntos o celdas que pueden organizarse también en triángulos. Esta eficiencia en la disposición se relaciona con principios geométricos vinculados a los números triangulares.
Cristales y minerales: Algunas formaciones cristalinas adoptan estructuras simétricas que evocan configuraciones triangulares, especialmente en minerales con crecimiento radial.
Una Red de Relaciones con Otros Números
Los números triangulares no existen en aislamiento. Al contrario, están profundamente entrelazados con otras familias numéricas que también se basan en formas geométricas:
Con los números cuadrados: Existen números que son simultáneamente triangulares y cuadrados, como el 1 o el 36. Estos números son raros y poseen una simetría especial que los hace muy atractivos desde el punto de vista teórico.
Con los números pentagonales y hexagonales: En ciertos casos, un mismo número puede pertenecer a varias secuencias figuradas. Por ejemplo, el número 210 es triangular, pentagonal y también hexagonal. Encontrar estos «números multi-figurados» es un desafío matemático que sigue despertando interés entre investigadores y aficionados.
Con los números primos: Aunque los números triangulares no son necesariamente primos, existen vínculos interesantes. Por ejemplo, se ha estudiado si ciertas operaciones entre números primos dan como resultado un número triangular. Esta relación es un área de investigación abierta en teoría de números.
Presencia en Juegos y Rompecabezas
Los números triangulares también hacen apariciones inesperadas en el mundo de los juegos, especialmente en aquellos que requieren estrategia o manipulación de objetos:
Bolos (bowling): En este deporte, la disposición de los 10 bolos en la pista responde a una configuración triangular perfecta (un triángulo de 4 filas: 1+2+3+4 = 10). Este no es un simple capricho, sino un diseño que permite distribuir el peso y la energía del impacto de forma eficiente.
Triángulos mágicos: Algunos rompecabezas numéricos distribuyen números en formas triangulares buscando que la suma de los lados dé un mismo resultado, algo así como una versión triangular del cuadrado mágico. Este tipo de pasatiempo utiliza la estructura de los números triangulares como base para desafiar la lógica del jugador.
Aplicaciones Informales en la Vida Cotidiana
En la vida diaria, aunque no nos demos cuenta, usamos patrones triangulares con frecuencia:
Organización de objetos: Al apilar vasos, pelotas o naranjas, muchas veces optamos de forma intuitiva por una configuración triangular, porque ofrece estabilidad y uso eficiente del espacio. Esta disposición responde a principios básicos que también rigen los números triangulares.
Jerarquías y niveles: En esquemas organizacionales o piramidales (como algunas estructuras militares, corporativas o incluso esquemas de juego), los niveles suelen aumentar en número siguiendo una progresión triangular: el primer nivel tiene una persona, el segundo dos, el tercero tres, y así sucesivamente. Este patrón permite expandir una red sin perder la simetría.
En la Historia de las Matemáticas
Los números triangulares fueron estudiados ya por los matemáticos de la Antigua Grecia. Pitágoras y sus discípulos, por ejemplo, veían en ellos una representación mística de la armonía. Para los pitagóricos, el número 10 —la suma de los cuatro primeros números naturales y, por tanto, un número triangular— tenía una importancia especial y se consideraba perfecto.
También aparecen en textos de matemáticos indios y árabes, que exploraron sus propiedades en el contexto de los números figurados y la resolución de problemas aritméticos y algebraicos. A lo largo de la historia, los números triangulares han servido como base para ilustrar ideas fundamentales en matemáticas recreativas y formales por igual.
Los Números Triangulares en Civilizaciones Antiguas
Babilonios: Utilizaban números triangulares en sus cálculos astronómicos hace más de 4,000 años.
Egipcios: Las pirámides incorporan proporciones basadas en números triangulares en su construcción.
Mayas: Sus calendarios utilizaban ciclos que involucran números triangulares.
Literatura y Arte
«La Divina Comedia» de Dante: La estructura de 100 cantos (más introducción) suma 101, y contiene referencias numéricas que involucran números triangulares.
Arquitectura Gótica: Las rosetones de las catedrales frecuentemente incorporan patrones basados en números triangulares.
Récords y Extremos Numéricos
El Número Triangular más Grande Calculado: Record actual: T₁₀¹²⁰ (número con más de 10²⁴⁰ dígitos) Aplicación: Verificación de límites en teoría de números computacional
Conclusión: el impacto duradero de los números triangulares
Los números triangulares representan mucho más que una curiosidad matemática; son una ventana hacia la comprensión profunda de cómo las matemáticas conectan conceptos aparentemente dispares. Desde su descubrimiento por los antiguos griegos hasta sus aplicaciones en la computación cuántica moderna, estos números han demostrado una relevancia y utilidad extraordinarias.
Su estudio nos enseña que las matemáticas más hermosas son a menudo las más útiles, y que la búsqueda de patrones y conexiones puede llevar a descubrimientos inesperados. Los números triangulares continúan inspirando nuevas investigaciones y aplicaciones, demostrando que incluso los conceptos matemáticos más antiguos pueden tener impactos revolucionarios en nuestro mundo moderno.
La próxima vez que veas una disposición triangular en la naturaleza, en el arte, o en un problema computacional, recuerda que estás observando una manifestación de uno de los patrones matemáticos más fundamentales y elegantes que conocemos. Los números triangulares no son solo números; son una puerta de entrada hacia la comprensión de la estructura matemática subyacente del universo.
¿Qué te ha parecido esta inmersión en el mundo de los números triangulares? ¿Conocías ya estos interesantes números o has descubierto algo nuevo hoy? ¿Conoces alguna otra curiosidad o aplicación de los números triangulares que te gustaría compartir? ¡Nos encantaría leer tus comentarios!