Tiempo estimado de lectura: 12 minutos | Matemáticas |
La constante de Euler: el número mágico del crecimiento y la naturaleza
Seguro que conoces a Pi (π), ese número enigmático que aparece siempre que hay un círculo de por medio. Pero el universo de las matemáticas tiene otros protagonistas igual de fascinantes, y uno de ellos es la constante de Euler, representada por la letra e. Con un valor aproximado de 2.71828, este número irracional y trascendental no es simplemente una curiosidad matemática: es una pieza fundamental en la estructura misma del crecimiento y el cambio continuo en la naturaleza.
A diferencia de otros números que encontramos en el día a día, e emerge de manera natural en fenómenos donde el crecimiento no se produce de forma lineal, sino exponencial. Imagina un bosque en expansión, una población de bacterias duplicándose sin pausa, o una inversión financiera que crece de manera constante gracias al interés compuesto. En todos estos procesos, e aparece como el hilo conductor que modela su evolución.
La magia de e reside en que no se limita a un campo en particular: está presente en la biología, describiendo el crecimiento de poblaciones; en la economía, calculando intereses compuestos; en la física, modelando procesos de desintegración y atenuación de señales; y en la informática, optimizando algoritmos y redes neuronales. Es un número universal, un símbolo del cambio perpetuo y un reflejo de cómo la naturaleza se organiza y evoluciona de forma constante y precisa.
Descubrir el valor de e es abrir una puerta a un mundo donde el crecimiento continuo y la expansión infinita son posibles, un concepto tan mágico como real. ¿Te atreves a conocer su historia y sus aplicaciones?
¿Pero qué es la constante e? – La explicación para niños
Imagina que tienes una planta mágica que crece sin parar. Cada día, crece un poco más que el anterior, y su crecimiento nunca se detiene. La constante e es un número especial que nos ayuda a entender cómo crecen cosas como esta planta mágica. Su valor es aproximadamente 2.71828, y aparece en muchas situaciones donde algo crece o cambia continuamente, como el dinero en el banco que gana intereses o una población de conejitos que se multiplica rápidamente.
Desentrañando el misterio de e
Para entender realmente qué es e, primero hay que conocer su relación con los logaritmos naturales. Imagina un número tan especial que se convierte en la base perfecta para modelar el crecimiento continuo en la naturaleza y la economía. Ese número es e, y su magia se esconde en la forma en que crece y se expande.
Cuando hablamos de logaritmos, generalmente pensamos en potencias de un número base. Por ejemplo, si decimos que log10(10)=1, significa que el 10 elevado a 1 es igual a 10. En el caso de e, su logaritmo natural, representado como ln(e), también es igual a 1:
ln(e)=1
Esto convierte a e en la base natural para muchos cálculos, sobre todo aquellos que implican crecimientos y cambios continuos. Pero, ¿qué significa realmente ese «crecimiento continuo»?
Un ejemplo intuitivo: el interés compuesto
Imagina que tienes 1 € y lo inviertes en un banco al 100% de interés anual. Si el interés se aplica una sola vez al año, al finalizar el periodo tendrás 2 €. Un rendimiento considerable. Pero, ¿qué pasaría si el interés se capitalizase dos veces al año? Al cabo del primer semestre tendrías 1.5 €, y al finalizar el segundo semestre, los intereses se aplicarían sobre esos 1.5 €, llevándote a un total de 2.25 €.
¿Qué ocurriría si el interés se aplicase cada mes? O mejor aún, ¿cada día? Cuanto más frecuente sea la capitalización, más se incrementa el valor total al final del año. Esta es la verdadera magia de e: si el interés se aplica de forma continua, sin descanso, el valor de tu inversión se acercaría a un número muy especial: 2.71828…, es decir, el valor de e.
La expresión matemática de e
Esta idea de crecimiento continuo se expresa de forma elegante en matemáticas con un límite:
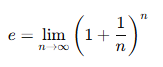
Lo que esta fórmula representa es exactamente eso: cuanto más dividimos el tiempo en pequeños fragmentos para aplicar el interés, más nos acercamos al valor de e. Imagina un reloj que marca el paso del tiempo, pero cada tic es una oportunidad para añadir un poco más de crecimiento. Cuanto más rápido marque ese reloj, más cerca estaremos de alcanzar el máximo crecimiento posible, y ese valor converge siempre en e.
Un número que modela el cambio perfecto
No importa si hablamos del crecimiento de una población, la expansión de una inversión o el ritmo de descomposición radiactiva: si el cambio es constante y continuo, estará modelado por e. Por eso se considera la base natural para describir el crecimiento exponencial, ese tipo de crecimiento que no sigue una línea recta, sino una curva que se dispara hacia el infinito.
En resumen, e es mucho más que un número: es una ley universal que describe cómo las cosas crecen y se transforman cuando no encuentran límites en su expansión. Es la firma del cambio continuo y el motor invisible de muchos fenómenos naturales y económicos.
e y su conexión con el infinito ♾️
La constante de Euler, e, tiene una relación mágica con el infinito. Imagina un proceso de crecimiento que no se detiene nunca, que avanza de forma continua, sin pausas ni límites. Esa idea de expansión infinita, de algo que crece eternamente, es precisamente lo que e representa.
Para entenderlo, piensa en un panadero que cada día amasa un poco más de pan que el anterior. Si cada día multiplicase la cantidad amasada por un pequeño porcentaje, el total crecería poco a poco. Ahora imagina que en lugar de hacerlo una vez al día, lo hace cada hora, cada minuto, cada segundo… de manera continua. Aunque parezca imposible, esa cantidad no crecería sin fin, sino que se estabilizaría en un valor muy preciso: 2.71828…, el valor de e.
La omnipresencia de e: un universo de aplicaciones
La verdadera fuerza de e no solo radica en su valor numérico, sino en su sorprendente capacidad para emerger de manera natural en multitud de campos del conocimiento. Desde la física y la biología hasta las finanzas y la ciencia de datos, e actúa como un hilo conductor que conecta conceptos aparentemente dispares. Es un número que describe el crecimiento continuo, el cambio exponencial y la evolución de sistemas complejos. A continuación, vamos a explorar los lugares donde e despliega todo su poder y muestra su versatilidad única.
e en el corazón del cálculo
Si hay un territorio donde e brilla con luz propia, es en el cálculo diferencial e integral. La función exponencial eˣ tiene una propiedad mágica: su derivada y su integral son exactamente iguales a la función original. Dicho de otro modo, la velocidad a la que crece eˣ en cada punto es igual a su propio valor en ese instante. Este fenómeno es único y convierte a e en el modelo perfecto para describir procesos de crecimiento continuo.
Esto significa que, si un sistema crece en proporción a su tamaño actual (poblaciones, inversiones, reacciones químicas), la función exponencial basada en e es la representación más pura y precisa de ese cambio.
Además, e es el protagonista de una de las identidades matemáticas más bellas y sorprendentes jamás descubiertas: la identidad de Euler. Esta ecuación, que relaciona las cinco constantes matemáticas más importantes, es un verdadero poema matemático:
eiπ + 1 = 0
En una sola expresión, aparecen el número de Euler (e), la constante de pi (π), el imaginario (i), el uno y el cero, los pilares fundamentales de las matemáticas. Es como si todos los elementos esenciales del universo matemático se dieran la mano en una armonía perfecta.
e en las finanzas y la economía
En finanzas, e impulsa el interés compuesto continuo. La fórmula A = P * ert calcula el valor futuro de una inversión con capitalización ininterrumpida, esencial para modelos avanzados y para comparar productos financieros.
Donde:
A es el valor final de la inversión,
P es el capital inicial,
r es la tasa de interés anual,
t es el tiempo en años.
Gracias a esta fórmula, los bancos y los economistas pueden calcular el valor futuro de inversiones que crecen sin pausas, una herramienta indispensable para comparar productos financieros y evaluar riesgos.
No solo en inversiones, e también se utiliza en la valoración de opciones financieras (Modelo de Black-Scholes) y en la predicción de fluctuaciones en el mercado. Modelos de riesgo, como los de VaR (Value at Risk), dependen de su comportamiento para anticipar cambios continuos en los precios de los activos.
e en la probabilidad y la estadística
La constante de Euler también es un pilar en la teoría de la probabilidad. Uno de los ejemplos más claros es la distribución de Poisson, que describe la probabilidad de un número determinado de eventos en un intervalo de tiempo fijo. Si quieres saber cuántas llamadas entrarán en un call center por hora, o cuántos coches pasarán por un peaje en un día, e es la clave para hacer ese cálculo.
Además, e está presente en la famosa distribución normal o «campana de Gauss». Esta curva, que aparece constantemente en estudios estadísticos, describe cómo se distribuyen datos como la altura de las personas, los errores de medición, o incluso los resultados de un examen en un grupo grande. En su ecuación matemática, e garantiza que la dispersión y el comportamiento de los datos sigan un patrón predecible y coherente.
e en la ciencia de la computación
En informática, e aparece en el análisis de algoritmos con crecimiento exponencial y en funciones de activación de redes neuronales, como la sigmoide, que permiten modelar comportamientos complejos. En la teoría de la información, los logaritmos en base e son la elección «natural» por sus propiedades matemáticas, simplificando la cuantificación de la información y el análisis de datos.
e en la física y la ingeniería
Desde la ley de enfriamiento de Newton hasta la carga de condensadores o la desintegración radiactiva, e modela innumerables fenómenos físicos. Las ecuaciones que describen la atenuación de señales, las vibraciones amortiguadas o el comportamiento de circuitos eléctricos a menudo incluyen funciones exponenciales con base e, siendo una herramienta crucial para ingenieros y físicos al describir el mundo real.
Un número que explica el cambio continuo en todo lo que nos rodea
La constante de Euler, e, está en el corazón de procesos fundamentales del mundo real. Es una constante que modela el crecimiento, el cambio y la evolución de una manera que pocos números pueden igualar. Allá donde algo crece de forma continua, donde una población se expande sin frenos o donde un interés se capitaliza sin pausas, e está ahí, describiendo el proceso con una precisión matemática casi mágica.
¿Sabías que la constante e está en todos lados aunque no la invites?
Es como ese colega que aparece en todas las fiestas sin que nadie sepa quién lo llamó, pero al final todos lo quieren. Así es e: una constante misteriosa que vale más o menos 2,718, y que aparece donde menos te lo esperas.
📈 Por ejemplo, imagina que metes 1 euro en el banco con un 100 % de interés. Si el interés se aplica una sola vez al año, acabas con 2 euros. Bien. Pero si lo aplican cada mes, mejor. ¿Cada día? Aún más. Si el banco se volviera loco y aplicara intereses cada segundo, al final del año tendrías unos 2,718 euros. Boom: ahí está e, colándose en tus ahorros.
☕ Otro ejemplo: estás tomando un café y lo dejas olvidado porque te pusiste a ver memes de gatos. Cuando vuelves, está frío. Pues bien, la fórmula que describe cómo se enfría ese café también lleva a e metida entre sus cálculos. No es magia, es matemáticas.
🧬 ¿Y la descomposición radiactiva? También e. Cuando un átomo decide que ya tuvo suficiente y se desintegra, la velocidad a la que eso pasa sigue una fórmula que… sí, otra vez, usa e. O sea, si los átomos tuvieran un grupo de WhatsApp, e estaría en todos los mensajes.
🎲 Incluso aparece en cosas tan raras como el juego del «amigo invisible». Imagínate que todos tiran los nombres en una bolsa, nadie puede sacarse a sí mismo y todos acaban con un regalo de otro. Si repites esto muchas veces, en promedio, alrededor del 37 % de las veces nadie acierta su propio nombre. ¿Adivina qué número representa ese 37 %? Exacto: 1/e.
✨ Y lo más loco: si haces la función eˣ, y le sacas la derivada (o sea, cómo cambia), da como resultado ella misma. ¡Ni se inmuta! Es como si te cortaras el pelo y te creciera al instante igualito. Pura elegancia matemática.
e: Más que un número, una ventana al universo
A lo largo de este recorrido hemos visto cómo e se manifiesta una y otra vez en lugares sorprendentes: desde el crecimiento de una inversión en un banco, hasta el enfriamiento de un objeto caliente o la propagación de una señal eléctrica. Pero, ¿qué tiene de especial este número? ¿Por qué aparece de forma natural en tantas áreas diferentes?
La constante de Euler, e, es mucho más que una simple cifra; es una llave maestra para comprender el cambio continuo en nuestro universo. Su valor, aproximadamente 2.71828, es solo la punta del iceberg. Lo verdaderamente asombroso de e es su capacidad para modelar procesos en los que el crecimiento, la expansión o la disminución se producen de manera constante y sin interrupciones.
La firma del crecimiento continuo
Para entender su magia, imagina un bosque creciendo sin descanso, una colonia de bacterias duplicándose sin freno o una inversión en un banco que acumula intereses de forma constante. En cada uno de estos casos, el aumento no se produce de manera discreta (como en un escalón), sino de forma continua, como una curva que se va elevando suavemente y sin pausas. Esta forma de crecer, de multiplicarse sin detenerse, es la esencia de e.
El concepto de capitalización continua es un claro ejemplo de cómo e modela la realidad. Si un capital se invierte con un interés compuesto que se aplica continuamente (cada segundo, cada milisegundo…), el valor resultante al final del periodo se aproxima a un múltiplo exacto de e. Esto no es una simple coincidencia, es una ley matemática que describe el crecimiento óptimo en condiciones ideales.
Un hilo conductor en el universo
Lo realmente fascinante es que esta constante trasciende las finanzas y aparece allí donde hay un proceso que evoluciona de manera natural y constante. En la biología, e modela cómo crecen las poblaciones de organismos, cómo las células se dividen y cómo los virus se propagan. En la física, describe el decaimiento de materiales radiactivos y el comportamiento de las ondas de luz y sonido al atravesar distintos medios.
Y no solo eso: la ecuación mágica de Euler, eiπ + 1 = 0, revela una conexión oculta entre las matemáticas puras y el comportamiento del universo. Relaciona el número imaginario ii, la constante π, el número e, el uno y el cero. En una sola expresión se sintetiza la estructura matemática del cosmos. Es una puerta que conecta el álgebra, la trigonometría y el análisis matemático de una forma casi mística.
Un lenguaje universal para describir el cambio
Lo maravilloso de e es que no importa el contexto: si algo crece, decae, se expande o se reduce de manera continua, e estará ahí para describirlo. La naturaleza parece haberlo elegido como su lenguaje secreto para expresar el cambio.
Cuando un río erosiona una roca poco a poco.
Cuando un virus se multiplica dentro de un organismo.
Cuando la luz pierde intensidad al atravesar una atmósfera densa.
Cuando el valor de una criptomoneda fluctúa en tiempo real.
En todos esos casos, la constante de Euler describe, con una precisión asombrosa, cómo se desarrollan estos procesos en el tiempo.
Un número que conecta lo visible y lo invisible
La verdadera magia de e es que actúa como un puente entre lo que podemos ver y lo que no. Nos permite modelar fenómenos invisibles al ojo humano, pero que existen y son medibles. Es la herramienta con la que los científicos exploran el microcosmos y el macrocosmos, desde el comportamiento de una partícula subatómica hasta la expansión de las galaxias.
e no es solo un número, es una ventana al orden oculto de la naturaleza, una firma matemática que aparece una y otra vez en los procesos de cambio. Cuando miras un bosque crecer, una ciudad expandirse o un río desgastar una montaña, e está ahí, invisible pero presente, dictando las reglas de ese crecimiento constante.
Y tú, ¿qué te parece esta fascinante constante? ¿Conocías todas estas aplicaciones de e o te ha sorprendido alguna en particular? Me encantaría leer tus experiencias y reflexiones en los comentarios. ¡Anímate a compartir!




